Unifying Behavioral and Evolutionary Ecology

In evolutionary ecology, we assume for a stationary population that natural selection favors phenotypes that maximize the total expectation of lifetime reproductive success R. This is equivalent to maximizing total expectation of remaining lifetime reproductive success for each age class x, R_x.  R_x is given by the following equation,

where x represents a particular age class, t is the index of age classes from x to infinity, l_t is the probability of survival from birth to age t, l_t / l_x is the probability of survival from age x to age t, and m_t is the expected reproductive success at age t. 

For newborns, x is zero, and the total expectation of lifetime reproductive success of a newborn simplifies to,

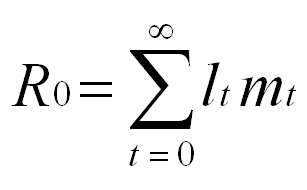
which is also known as the net replacement rate of the population (l₀ , the probability of surviving from age 0 to age 0, is one by definition).

For an individual aged x, we can partition R_x into present and future reproduction by taking (l_t / l_x) m_t outside the summation sign for age class x (i.e. for t=x), which results in the following.

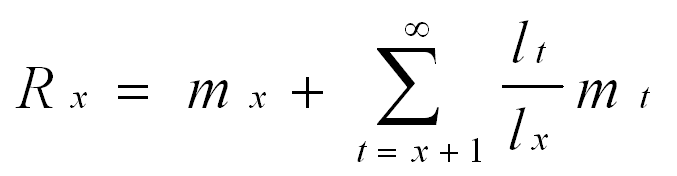
Present reproduction at age x is represented by m_x (the age class in question); whereas, future reproduction from age x+1 to infinity is represented by what is contained in the summation. To make this expression for R_x more transparent, we resort to a little trickery, where we multiply the term in the summation sign by 1 (i.e. by l_x+1 / l_x+1) and then simplify.

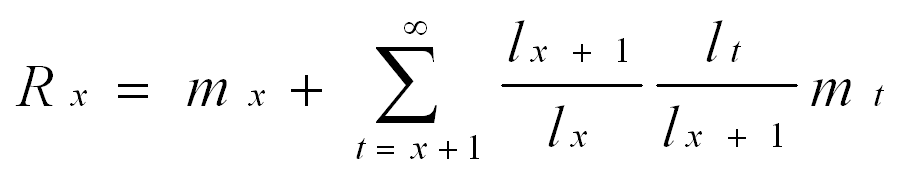
Because x is a constant for the age class under consideration, we can take l_x+1 / l_x outside the summation.

The term, l_x+1 / l_x , represents survival from x to x+1, and the term in the summation now becomes R_x+1 , and the equation now looks as follows.

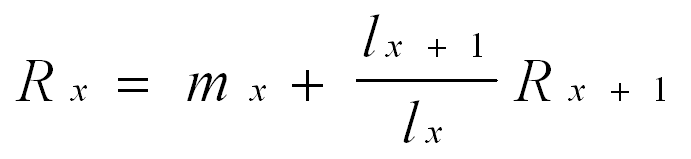
Thus, the total expectation of remaining lifetime reproductive success of an individual aged x is equal to reproductive success at age x (m_x) plus the probability of survival from age x to x+1 (l_x+1 / l_x) times the total expectation of remaining lifetime reproductive success of an individual aged x+1 (R_x+1).

This equation is basically Williams' (1966) "refinement of Lack's principle," which is the foundation for life history theory. This equation can be modified to incorporate behavioral ecology in two ways. 

1. By making its fitness components, e.g. present versus future reproduction, state dependent, we can examine specific classes of animal behavior, e.g. feeding, hiding, courtship, parental care, as investment into one or more components of fitness. For example, present reproduction, m_x, can be divided into two terms that reflect Lack's tradeoff between offspring quantity versus offspring quality; whereas, Williams' tradeoff is between present and future reproduction. Mating can be viewed as an investment into offspring quantity, parental care can be viewed as an investment into offspring quality, and feeding can be viewed as an investment into parent survival from x to x+1.

2. The time scale, x,  can be whatever is appropriate for a particular question, such as breeding season, brood cycles within breeding season, or days within a brood cycle. If, for example, x represents days within a brood cycle,  then present reproduction is measured in terms off offspring that fledge today, and future reproduction includes future fledging within the current brood cycle, future brood cycles within the current breeding season, and future breeding seasons.

Marc Mangel; Colin W. Clark 1986. Towards a Unified Foraging Theory. Ecology 67: 1127-1138. 

John M. McNamara; Alasdair I. Houston 1986. The Common Currency for Behavioral Decisions. American Naturalist 127: 358-378.