Hawks & Doves

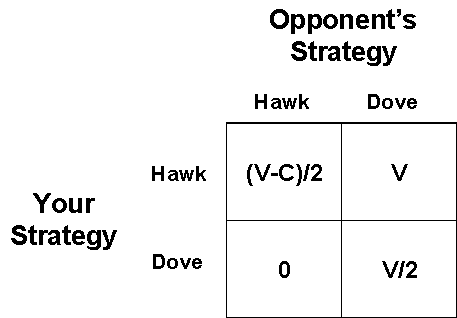
The Hawks & Doves game is an example of a two player game, where each player is assumed to be identical in competitive ability. In other words, it's a symmetrical contest. The two players compete for a resource, and the fitness obtained from an encounter is proportional to the payoff each player receives. Hawks are willing to risk injury in an escalated contest; whereas, Doves are not. Let V = the value of a contested resource, and C = the cost of escalation. Below appears the payoff matrix, where the elements in the matrix are 'your' payoffs. 

Figure 1. The Payoff Matrix.

The decision variable is P_H; that is, the contestants choose a probability of playing Hawk, P_H, for any encounter with an opponent. The object of the game is to find an evolutionarily stable strategy (ESS) for P_H for the population, such that when it's common it cannot be invaded by a rare mutant alternative strategy.

The fitnesses of the two strategies are given by:

W_H = P_H (V-C)/2 + (1 - P_H) V

and 

W_D = P_H 0 + (1 - P_H) V/2

To solve this game graphically, we plot our Fitnesses, W_H and W_D, versus Hawk Frequency, P_H. For any given level of P_H, if W_H > W_D, then P_H increases; if W_H < W_D, then P_H decreases, and if W_H = W_D, then P_H remains constant. Once P_H stops changing, either because it has been driven to 0 or 1, or because W_H = W_D, then we have reached the evolutionarily stable strategy, or ESS. 

There are two cases to this problem.

Case 1: V > C. If we let V = 10 and C = 5, then we can solve this numerical example graphically, which appears below.

Figure 2. Fitnesses, W_H and W_D, versus Hawk Frequency, P_H, for the case of V = 10 and C = 5.

In this case, for all values of P_H, W_H >  W_D, therefore P_H keeps increasing until it equals 1, which is the pure ESS. 

Note that if the population consisted of pure Doves, that population fitness would be 5, but that at the ESS of pure Hawks, population fitness is 5/2. In this case, the average fitness of the population is minimized! Average fitness is given by...

WBar = W_H P_H + W_D (1 - P_H)

Case 2: V < C. If we let V = 4 and C = 5, then we can solve this numerical example graphically as well; the solution appears below.

Figure 3. Fitnesses, W_H and W_D, versus Hawk Frequency, P_H, for the case of V = 4 and C = 5.

In this case the two fitness functions cross. To the left of the intersection point, W_H > W_D, and P_H increases, but to the right of the intersection point, W_H < W_D, and P_H decreases. Consequently, the intersection point is a Mixed ESS, which says in each encounter play Hawk with probability of 0.8, which gives a population that plays Hawk 80% of the time.

We can solve for the ESS directly by setting our two fitnesses equal to each other.

At P_H *, 

W_H = W_D  

or

P_H (V-C)/2 + (1 - P_H) V = P_H 0 + (1 - P_H) V/2 .

If we solve this expression P_H*, we get

P_H * = V/C

For V = 4 and C = 5, this means that  P_H * = 0.8. Note that if V > C, then P_H * = 1.0.